Chương VI: Mặt phẳng biểu diễn trở kháng thường hóa và các yếu tố ảnh hưởng

VI.1. Ôn tập- điện trở kháng của cuộn dây riêng biệt.
Chúng ta đã biết ở chương 2 rằng cuộn dây dạng phẳng hoặc ống dây có thể được coi như các điện trở thuần Ro và độ tự cảm Lo được mắc nối tiếp với nhau.
Sơ đồ điện như sau:

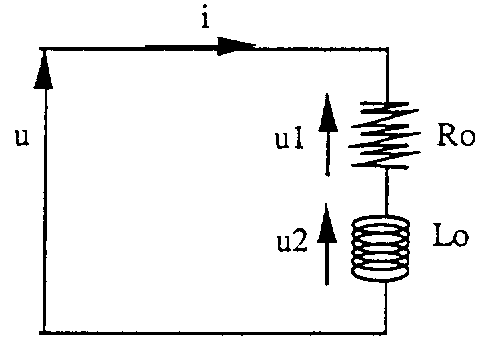
Chúng ta cũng biết rằng trở kháng của mạch điện như vậy được biểu diễn (dạng số phức) bằng công thức sau:
Zo = Ro + j.Xo
Zo = Ro + j.Lo.
và có thể biểu diễn trên sơ đồ ( được gọi là mặt phẳng trở kháng) như sau:

Trong đó độ lớn của Zo bằng:
Zo =  (Ro2 + Lo2.2)
và pha  dược tính bởi:
tg = Lo./Ro
Zo tương ứng với trở kháng của cuộn dây riêng biệt tức là cuộn dây ở vị trí xa bất cứ vật dẫn nào.

Chúng ta gọi đó là trở kháng không tải hoặc ở trong không khí.
Trên thực tế và trong phần lớn các trường hợp, ta nhận thấy điện trở thuần của cuộn dây rất nhỏ so với điện kháng cảm ứng Xo và có thể bỏ qua trong tính toán.

Ta suy ra rằng trong thực tế:
Zo = Xo = Lo.
và
 = /2

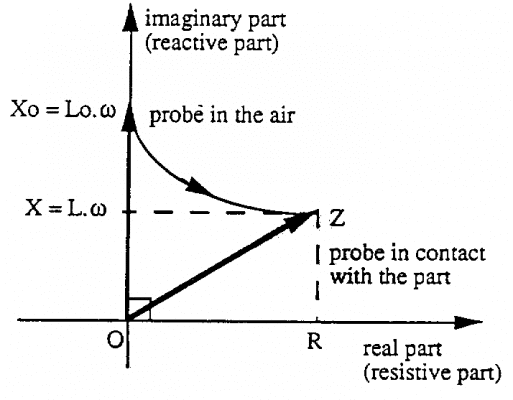
Từ đó trở kháng được biểu diễn trên mặt phẳng như sau:

VI.2. Trở kháng của cuộn dây khi tiếp xúc với vật dẫn
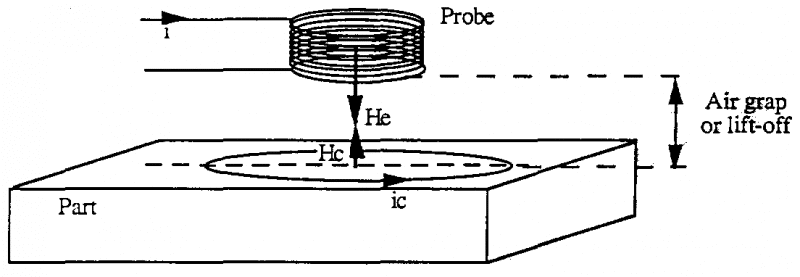
Khi cuộn dây như trên được đặt gần hoặc trên một vật dẫn, dòng điện xoáy được tạo ra trong vật dẫn bởi sự cảm ứng điện từ.

Mọi thứ sẽ chuyển dịch nếu như trở kháng của cuộn dây thay đổi khi chúng ta dịch chuyển nó tới gần vật dẫn. Giá trị Zo (chế độ không tải) sẽ thay đổi thành Z.

Trên thực tế, ta nhận thấy phần điện trở thuần và phần cảm ứng của cuộn dây thay đổi đông thời.

Ta có thể nói một cách đơn giản là:
– Sự thay đổi phần điện trở thuần của cuộn dây liên quan đến sự chuyển động của dòng điện xoáy vào trong vật dẫn và đặc biệt liên quan đến sự suy giảm năng lượng bời hiệu ứng Joule (tỉ lệ thuận với điện trở của vật và với bình phương cường độ dòng điện xoáy). Kết quả của sự thay đổi đó là phần điện trở thuần tăng lên. Giá trị thay đổi từ 0 lên R
– Sự thay đổi phần điện kháng cảm ứng của cuộn dây liên quan đến sự xuất hiện cảm ứng tương hỗ (xem chương 4) giữa cuộn dây và vật dẫn.
Từ trường Hc tạo bởi tạo bởi dòng điện xoáy ngược với từ trường sinh ra nó He. Nó làm cho phần điện kháng cảm ứng giảm từ giá trị Xo tới X.
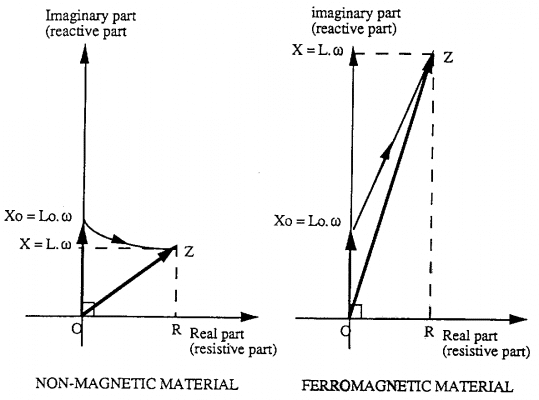
Sự thay đổi của trở kháng của cuộn dây được biểu diễn trên sơ đồ sau:

Ghi chú:
Đối với trường hợp vật liệu sắt từ, sự thay đổi trở kháng hoàn toàn khác.
Khi vật liệu đó chưa bão hòa, ta nhận thấy:
– Sự tăng phần điện trở thuần do hiệu ứng nhiệt liên quan dòng điện xoáy (hiệu ứng Joule), nhưng cũng liên quan tới sự quay các vùng từ (domains) dưới tác động của từ trường xoay chiều tạo bởi cuộn dây.
– Sự thay đổi phần điện trở thuần khi vật dẫn là sắt từ nói chung là nhỏ hơn so với vật liệu không từ tính.
– Sự tăng mạnh của phần điện kháng cảm ứng liên quan đến sự tăng mạnh độ tự cảm của cuộn dây do độ từ thẩm cao của vật liệu sắt từ. Độ tự cảm của cuộn dây xấp xỉ tăng r lần:
L = . N2.S/l = r.o.N2.S/l = r.Lo

VI.3. Trở kháng thường hóa hay rút gọn:
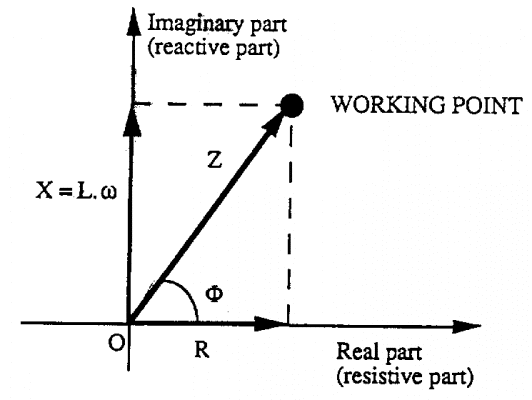
Chúng ta gọi điểm hoạt động là điểm đầu mút của vectơ trở kháng Z trên sơ đồ trở kháng.

Trên sơ đồ biểu diễn trở kháng trước đây ta thấy điểm hoạt động ở chế độ không tải (trong không khí) phụ thuộc vào trở kháng của đầu dò Zo (cụ thể là độ tự cảm Lo) và tần số kiểm tra (cụ thể là ).

Bất cứ thay đổi của trở kháng liên quan đến sự xuất hiện vật dẫn tới gần làm cho điểm hoạt động trên sơ đồ trở kháng sẽ dịch chuyển phụ thuộc vào Zo.

Cho nên để đơn giản sự biểu diễn trên sơ đồ trở kháng và đặc biệt là không phụ thuộc vào các điều kiện kiểm tra, có thể định nghĩa trở kháng Zn là trở kháng thường hóa hay còn gọi là trở kháng rút gọn.
Zn = Z/Zo
trong đó Zo = Lo.
nên Zn = R/Lo. + j.L. /Lo.

VI.4. Sơ đồ trở kháng thường hóa (rút gọn)
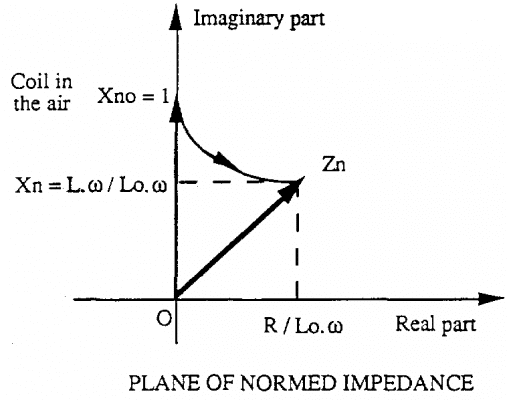
Từ giá trị Zn tính được ta có thể biểu diễn trở kháng trên sơ đồ như sau:

Sự biếu diễn này không phụ thuộc vào các điều kiện kiểm tra.

Ta đã biết trong trường hợp cuộn dây riêng biệt, trở kháng được tính theo công thức sau:
Zno = j.Xno

Điểm hoạt động nằm trên trục thẳng đứng (tương ứng phần điện kháng cảm ứng) tại điểm Xno = 1 (Ta nhớ rằng giá trị j của số phức bằng 1).

VI.5. Xây dựng sơ đồ trở kháng và các yếu tố ảnh hưởng
Có thể nghiên cứu sự dịch chuyển của điểm hoạt động trên sơ đồ trở kháng rút gọn để xem xét hiểu rõ sự ảnh hưởng của các yếu tố tới trở kháng của đầu dò..

Các yếu tố mà ta nghiên cứu có thể tương ứng với sự thay đổi tính chất của vật liệu (thay đổi độ dẫn điện, thay đổi độ từ thẩm), với sự thay đổi điều kiện kiểm tra (thay đổi tần số, khoảng cách giữa đầu dò và chi tiết), với sự thay đổi chiều dày chi tiết, trong sự hiện diện của lớp phủ trên bề mặt chi tiết, hoặc nếu có vài khuyết tật xuất hiện trong chi tiết (các vết nứt chẳng hạn).

Từ sự phân tích đó, sau đó có thể xây dựng sơ đồ trở kháng được thường hóa để thể hiện vị trí và sự dịch chuyển của điểm hoạt động.

Xây dựng sơ đồ trở kháng được thường hóa theo lý thuyết và tính đến sự thay đổi của các yếu tố liên quan thì rất phức tạp. Chính vì vậy chúng ta chỉ đề cập đến kết quả chung và tính chất định tính, nhưng cũng đủ để hiểu được nguyên lý các hiện tượng.

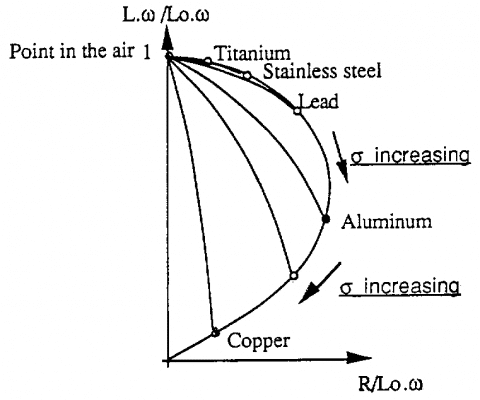
Sơ đồ dưới đây biểu diễn chung các vị trí của các điểm hoạt động đối với vật liệu không từ tính.

Để nắm được hình dạng chung của sơ đồ trở kháng, ta có thể xem xét vài điểm đặc biệt:
a) Điểm tọa độ (0,1)
Chúng ta đã biết rằng điểm tọa độ (R/Xo = 0, X/Xo = 1) tương ứng với trường hợp đầu dò để trong không khí.

Trong thực tế điểm đó cũng có thể tương ứng với trạng thái khác mỗi khi dòng điện xoáy ngừng chạy. Đó là các trường hơp:
– Chi tiết là vật liệu không dẫn điện, độ dẫn điện bằng không ( = 0)
– Dòng điện chạy qua đầu dò là dòng điện một chiều (tần số F = 0)

b) Điểm tọa độ (0,0)
Điểm này tương ứng với trạng thái đầu dò hoàn toàn không có trở kháng, khi đặt trên vật liệu, có nghĩa là không có phần điện trở thuần cũng như phần điện kháng cảm ứng. Điều này chỉ có thể xảy ra khi vật liệu là loại siêu dẫn, độ dẫn điện bằng vô cùng. Trong trường hợp đó, không có bất cứ sự suy giảm nào bởi hiệu ứng Joule liên quan đến dòng điện xoáy (phần điện trở thuần bằng không), và từ trường Hc tạo bởi dòng điện xoáy ngược với từ trường He sinh ra nó (phần điện kháng cảm ứng triệt tiêu).

Hiện tượng trên cũng có thể thấy khi làm việc với tần số rất cao, dòng xoáy chỉ có ở trên bề mặt chi tiết.

c) Điểm trung gian:
Chúng ta đã biết trước rằng sự có mặt của dòng điện xoáy thường dẫn đến sự tăng phần điện trở thuần (bởi hiệu ứng Joule) và giảm phần cảm kháng (bởi sự cảm ứng tương hỗ) khi so sánh vói điểm hoạt động ở trạng thái trong không khí (trường hợp của vật liệu không từ tính).

Chúng ta nhận thấy rằng nếu chúng ta chậm tần số kiểm tra (hoặc độ dẫn điện của vật liệu), các điểm hoạt động mô tả phần thứ nhất của đường cong AB. Ở phần này, phần điện trở thuần tăng chậm và phần cảm kháng thì giảm.

Sau một tần số nhất định (hoặc độ dẫn điện nhất định của vật liệu), có sự giảm chậm cả hai thành phần điện trở thuần và cảm kháng. Điểm hoạt động theo đường BO tới điểm tọa độ (0,0). Sự suy giảm đó liên quan đến sự tập trung (hiệu ứng bề mặt) của dòng điện xoáy.

5.1. Sự ảnh hưởng của độ dẫn điện:

Có thể kiểm chứng bằng thực nghiệm sự ảnh hưởng của độ dẫn điện  từ vị trí điểm hoạt động trong sơ đồ trở kháng rút gọn bằng cách đặt đầu dò lên các loại vật liệu khác nhau, có độ dẫn điện khác nhau.
Hãy tưởng tượng chúng ta thực hiện thực nghiệm đó chỉ với vật liệu phi từ tính; chúng ta nhận thấy, như đã mô tả ở phần trên, các điểm hoạt động nằm trên đường tạo thành hình cung của đường tròn.

Chúng ta ghi nhận từ hình dạng đó rằng quy trình kiểm tra với dòng xoáy có thể sử dụng để phân loại vật liệu.

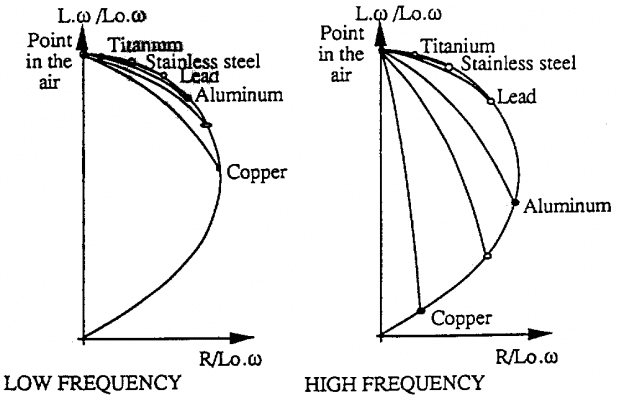
5.2. Ảnh hưởng của tần số:

Cũng bằng phương pháp đó, nếu chúng ta thực hiện các thực nghiệm với hai tần số khác nhau, chúng ta nhận thấy rằng các điểm hoạt động nằm trên đường cong, nhưng khoảng cách giữa các điểm phụ thuộc vào tần số.

Tần số càng cao thì khoảng cách giữa các điểm càng lớn.
Các điểm có chiều hướng chuyển dịch về điểm tọa độ (0,0).

Chúng ta thấy rõ từ các sơ đồ trên rằng nếu chúng ta muốn phân biệt hai vật liệu có độ dẫn điện gần giống nhau thì cần thiết phải kiểm tra với tần số cao.

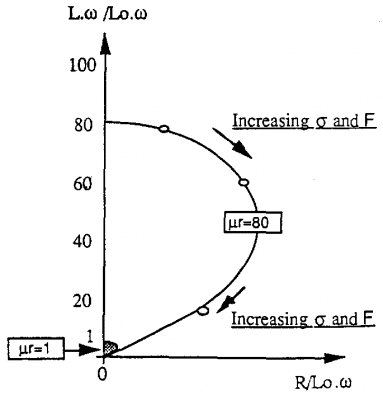
5.3. Ảnh hưởng của độ từ thẩm:
Khi vật dẫn là vật liệu sắt từ được đưa vào cuộn dây, độ tự cảm của cuộn dây tăng r lần.
So sánh với sơ đồ mà ta thu được từ vật liệu phi từ tính, chúng ta cũng lại thu được đường cong có cùng hình dạng nhưng chịu một hệ số khuyếc đại là r

r càng lớn thì đường cong của các điểm hoạt động càng lớn.
Ngoài ra chúng ta cũng thấy sự hoạt động giống như đối với vật liệu từ tính. Nếu chúng ta đặt đầu dò lên vật liệu sắt từ có cùng độ từ thẩm nhưng có độ dẫn điện tăng cao hơn, điểm hoạt động sẽ dịch chuyển chậm về phía dưới của đường cong.

Ta cũng sẽ thấy sự dịch chuyển như vậy khi ta tăng tần số.

Ghi nhận cuối cùng rằng chi tiết bằng sắt từ đôi khi thể hiện nhược điểm là có độ từ thẩm thay đổi (không là hằng số). Đó là vấn đề chính cho kiểm tra vì điểm hoạt động dịch chuyển rất lớn theo điểm mà ta quan tâm trên vật.

5.4. Ảnh hưởng của khe hở giữa đầu dò và chi tiết:

Chúng ta gọi khe hở là khoảng cách giữa đầu dò và chi tiết

Khe hở đó còn được gọi là: LIFT-OFF.

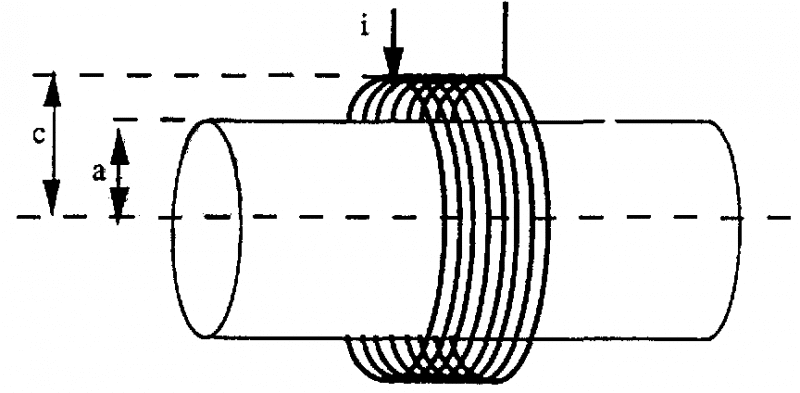
Trong trường hợp chi tiết hình trụ (thanh tròn hoặc ống tuýp) bằng ống dây, khe hở thường được đặc trưng bởi FILLING FACTOR (hệ số điền đầy).

Hệ số điền đầy được tính bằng công thức:
 = (a/c)2

trong đó: a là bán kính chi tiết
c là bán kính cuộn dây

từ đó suy ra 0    1

Chúng ta cũng nhận thấy rằng nếu đường kính của chi tiết bằng một nửa đường kính của đầu dò (a/c = 0.5), filling factor  = 0.25.

Trong trường hợp khe hở tăng (hoặc hệ số điền đầy giảm), thì hiện tượng cảm ứng điện từ sẽ giảm.

Độ nhạy của phép kiểm tra cũng giảm. Trong thực tế chúng ta nhìn thấy sự suy giảm đó rất nhanh nên cần thiết phải giữ khe hở nhỏ nhất có thể.

Nói cách khác, trong trường hợp kiểm tra chi tiết hình trụ bằng cuộn dây, filling factor phải lớn nhất có thể, gần giá trị 1 nhất.
Chúng ta có thể nhận biết trực giác khi sự tiếp xúc điện từ không đạt cực đại, nó không bao giờ có thể loại trừ cảm kháng của cuộn dây, kể cả khi kiểm tra chi tiết có độ dẫn điện lớn vô cùng.

Thực tế trong trường hợp đầu dò đặt xa chi tiết, một phần của từ trường He tạo bởi đầu dò không được sử dụng để tạo dòng điện xoáy. Những dòng điện xoáy đó không bao giờ có thể tạo ra từ trường Hc hoàn toàn đối kháng với He.
Chúng ta thấy đường cong đại diện cho các điểm hoạt động đó không đạt tới điểm tọa độ (0,0).

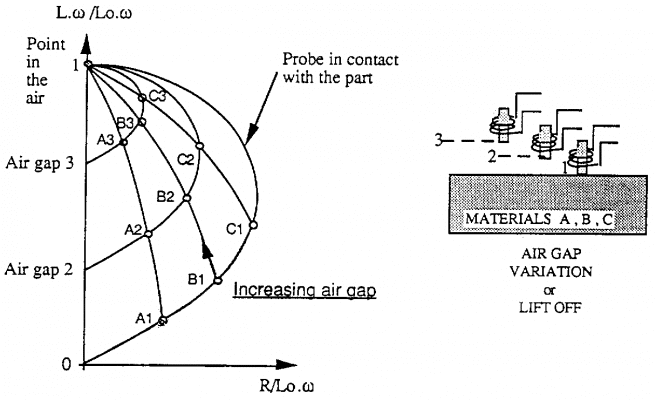
Đối với vật liệu cho trước (ký hiệu B trên sơ đồ), điểm hoạt động được mô tả bởi đường cong B1B2B3, theo sự tăng khe hở, cuối cùng gặp điểm (0,1) khi đầu dò đã tương đối xa chi tiết.

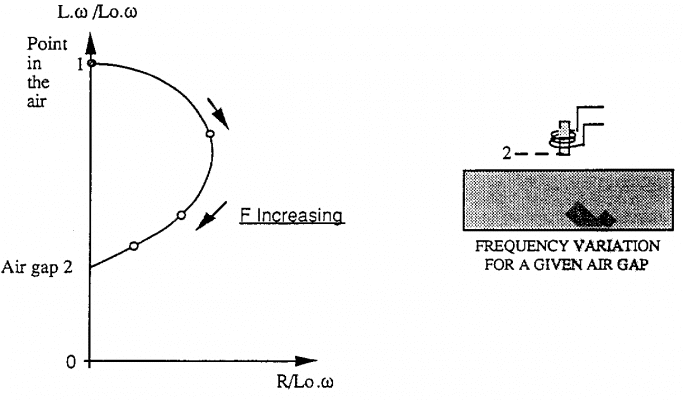
Bây giờ hãy tưởng tượng chúng ta thực hiện phép kiểm tra với khe hở định trước. Nếu chúng ta tăng tần số lên, điểm hoạt động sẽ chuyển động rất nhanh xuống phía dưới của đường cong tương ứng với khe hở đó.

Ghi chú:
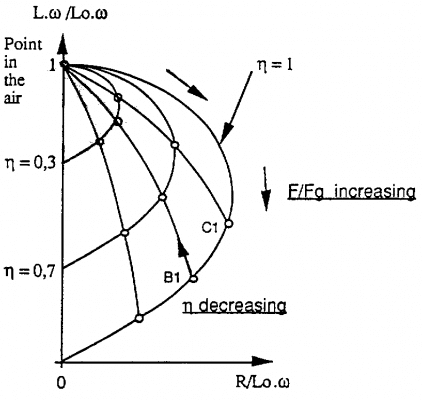
Trong trường hợp kiểm tra chi tiết hình trụ, chúng ta cũng thu được mạng lưới các đường cong như vậy.
Khe hở được thể hiện bằng hệ số điền đầy .
Chúng ta thấy điểm hoạt động cũng dịch chuyển khi thay đổi tần số.
Trong trường hợp đó, sự thay đổi tần số được biểu diễn bằng tỷ số F/Fg.

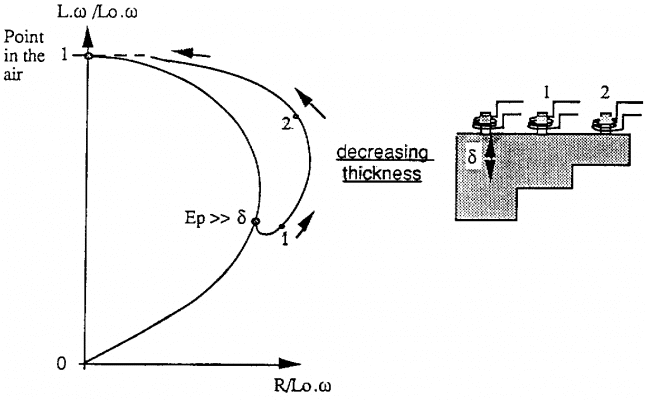
5.5. Ảnh hưởng của chiều dày chi tiết:
Chúng ta biết rằng dòng điện xoáy được đặc trưng bởi chiều sâu thẩm thấu quy ước .

Khi chiều dày chi tiết lớn hơn nhiều chiều sâu thẩm thấu quy ước  (trong thực tế nhiều hơn 3), kết quả thu được không phụ thuộc vào chiều dày chi tiết.

Khi chiều dày của chi tiết gần bằng hoặc nhỏ hơn chiều sâu thẩm thấu quy ước , ta thấy sự dich chuyển điểm hoạt động trên sơ đồ trở kháng.

Hiện tượng đó có thể diễn giải như là do khi ta ngừng cho dòng xoáy chạy trong chi tiết.

Trong trường hợp kiểm tra chi tiết phẳng với cuộn dây phẳng, sự dịch chuyển của điểm hoạt động theo chiều giảm liên tục của chiều dày chi tiết được biểu diễn như sau:

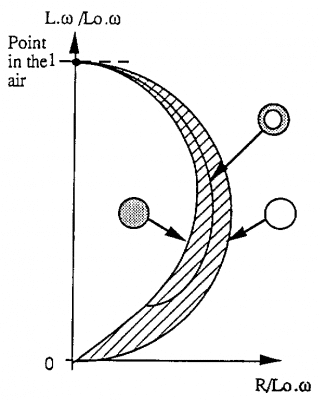
Trong trường hợp kiểm tra chi tiết hình trụ, kết quả tương tự cũng thu được đối với chi tiết hình ống mỏng vô cùng (di/de = 1), đường cong thu được cho hệ số điền đầy  = 1 là một nửa hình tròn.

Đường cong tương ứng cho thanh đặc hoặc ống dày nằm trong nửa đường tròn đó.
Đối với ống có chiều dày trung bình, đường cong nằm giữa hai đường trên (phần gạch).
Nó tương ứng xấp xỉ một phần của đường tròn khi cắt đường cong tương ứng với thanh đặc.

5.6. Ảnh hưởng của lớp phủ:

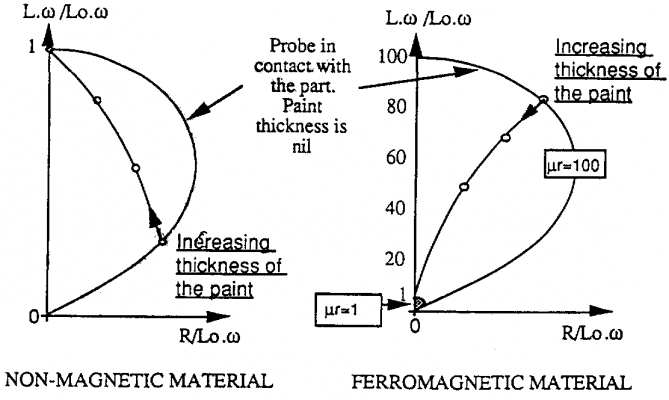
5.6.1. Lớp phủ không dẫn điện:

Trường hợp này tương ứng với chi tiết được sơn phủ.

Hiện tượng nhìn thấy giống như khi khe hở giữa đầu dò và chi tiết thay đổi. Chúng ta thu được sự biểu diễn sau đây khi chiều dày lớp phủ tăng lên.

5.6.2. Lớp phủ phi từ tính:

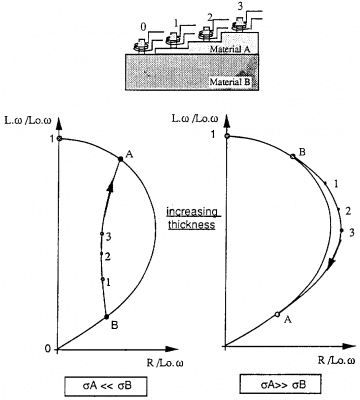
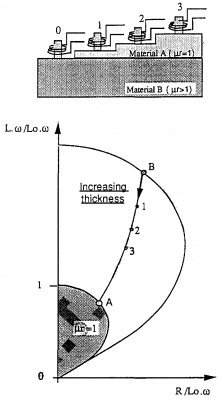
Ta tưởng tượng có một lớp phủ dẫn điện phi từ tính A được phủ lên vật liệu phi từ tính B.

Chúng ta có thể chỉ ra rằng nếu:
• A  B thì điểm hoạt động sẽ dịch chuyển từ B sang A khi chiều dày lớp phủ tăng lên. Điểm hoạt động sẽ nằm ngoài đường cong cho vật liệu phi từ tính (đường r = 1)

• A  B thì điểm hoạt động cũng sẽ dịch chuyển từ B sang A khi chiều dày lớp phủ tăng lên, nhưng nằm phía trong của đường cong r = 1.

Điểm hoạt động sẽ gặp điểm A khi chiều dày lớp phủ dày hơn rất nhiều chiều sâu thẩm thấu quy ước của dòng điện xoáy trong vật liệu đó.

Ta tưởng tượng có một lớp phủ dẫn điện phi từ tính A được phủ lên vật liệu từ tính B.
Ta thu được sơ đồ sau (theo chiều tăng của chiều dày lớp phủ).

5.7. Ảnh hưởng của khuyết tật:

5.7.1. Khuyết tật mở:

Hãy tưởng tượng chi tiết bằng vật liệu phi từ tính với khuyết tật nhân tạo là các vết nứt vuông góc mở trên bề mặt có độ sâu tăng dần Cd.

Ta giả thiết đầu dò tiếp xúc với chi tiết thật hoàn hảo (khe hở bằng không hoặc  = 1)
Ở vị trí không có vết nứt, điểm hoạt động nằm trên đường cong r = 1.
Ở các vị trí vết nứt, điểm hoạt động dịch chuyển theo các đườn Cd1, Cd2, Cd3. Vị trí Cd4 tương ứng vị trí đầu dò đặt trên cạnh của chi tiết giống như khi đó là vết nứt sâu.

Ta thấy rằng chiều dài và hướng dịch chuyển tương ứng với chiều sâu vết nứt.

5.7.2. Khuyết tật nằm trong:

Hãy tưởng tượng chi tiết bằng vật liệu phi từ tính với khuyết tật nhân tạo là các vết nứt ở trong chi tiết vuông góc với bề mặt có chiều dài cố định L và có độ sâu tăng dần Ci.

Chỉ có vết nứt 1 là mở và chiều dài L xấp xỉ chiều sâu thẩm thấu quy ước.

Ở các vị trí vết nứt, điểm hoạt động dịch chuyển theo các đườn Ci1, Ci2, Ci3. Vị trí Ci4 tương ứng vị trí đầu dò đặt trên vết nứt nằm sâu hơn nhiều chiều sâu thẩm thấu quy ước.

5.8. Tóm tắt:

Nói một cách ngắn gọn là sự dịch chuyển của điểm hoạt động tương ứng với tính chất yếu tố quan tâm.
Từ đó ta có thể lập một sơ đồ tổng quát như sau: