Chương V: Nguồn gốc và sự truyền của dòng điện xoáy
V.1. Nguồn gốc của dòng xoáy:
Chúng ta đã biết trong chương trước rằng hiện tượng cảm ứng điện từ tạo ra một số dòng điện trong dây dẫn khi dây dẫn này đưa vào từ trường thay đổi.
Từ trường thay đổi có thể tạo ra bằng cách, dịch chuyển dây dẫn vào từ trường, hoặc sử dụng từ trường thay đổi tạo bởi cuộn dây được cung cấp dòng điện xoay chiều.
Hiện tượng cảm ứng điện từ cũng xuất hiện khi ta thay dây dẫn bằng chi tiết làm bằng vật liệu dẫn điện.
Trong trường hợp đó, dòng điện cảm ứng trong vật liệu được gọi là dòng xoáy.
Như đã mô tả ở chương trước, dòng điện xoáy chạy trong vật liệu theo những đường cong và ngược với sự thay đổi của từ trường cảm ứng.
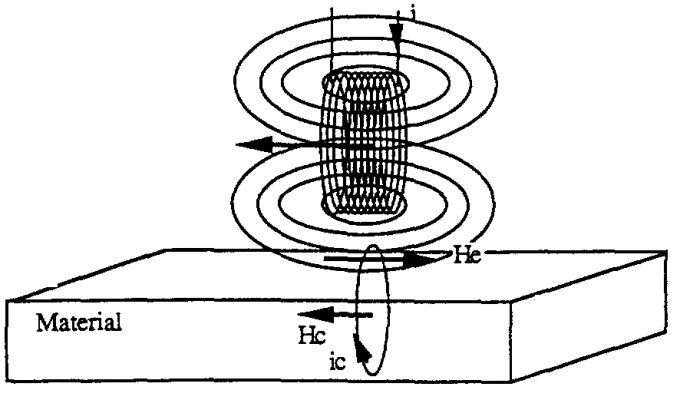
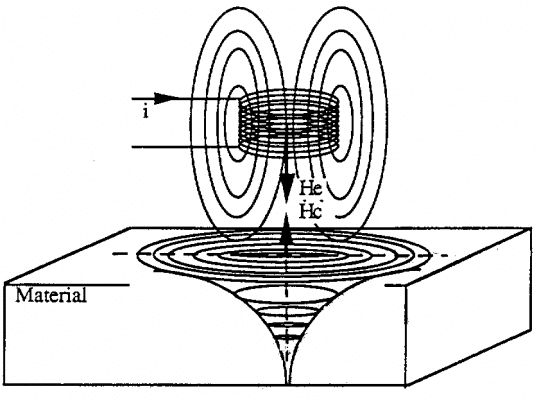
Nếu ta cho dòng điện xoay chiều i chạy trong cuộn dây cảm ứng vuông góc với bề mặt vật dẫn, dòng xoáy sẽ chạy theo các đường cong song song với bề mặt vật dẫn.
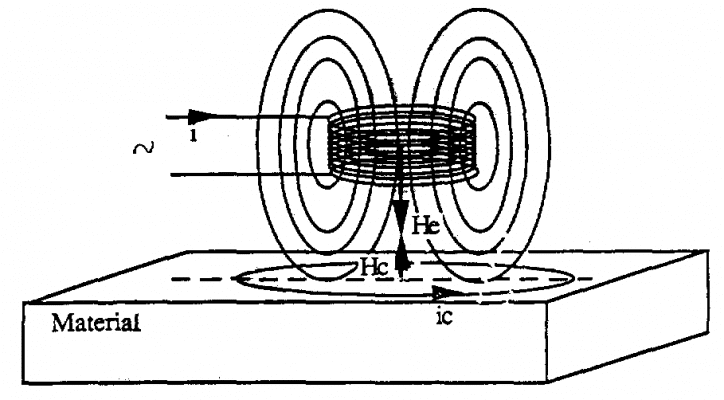 Nếu cuộn dây cảm ứng giống thế nhưng đặt song song với bề mặt vật dẫn, dòng xoáy ic sẽ chạy theo các đường cong vuông góc với bề mặt vật dẫn.
Nếu cuộn dây cảm ứng giống thế nhưng đặt song song với bề mặt vật dẫn, dòng xoáy ic sẽ chạy theo các đường cong vuông góc với bề mặt vật dẫn.
Như một nguyên tắc chung, dòng điện xoáy chạy song song với các vòng dây của cuộn dây cảm ứng.
Bên cạnh đó, dòng xoáy còn làm vật liệu nóng lên theo hiệu ứng Joule (chương III).
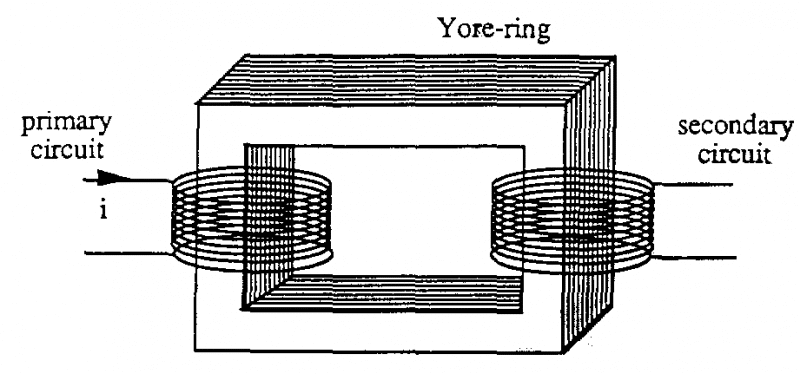
Trong một số ứng dụng (ví dụ máy biến thế), hiệu ứng đó có hại bởi nó làm tiêu hao năng lượng. Nên để giảm dòng xoáy chúng ta lắp ráp các miếng kim loại được sơn cách điện vào với nhau thành vòng gông, vuông góc với dòng điện xoáy. Thiết bị như thế chống lại dòng điện xoáy.
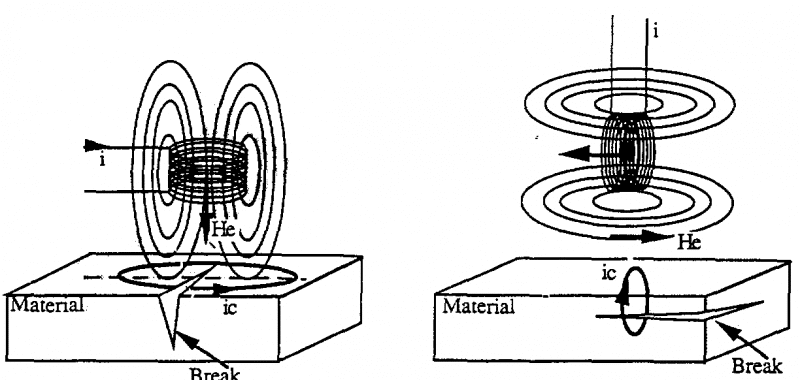
Từ ví dụ trên, chúng ta đưa ra kết luận rằng bất cứ bất liên tục nào trong vật liệu nằm vuông góc với đường chạy của dòng xoáy sẽ ngăn cản chúng.
Kiểm tra với phương pháp dòng xoáy bao gồm tạo chúng trong vật cần kiểm tra bởi cuộn dây phẳng hay ống dây có dòng điện xoay chiều chạy qua, có những dòng xoáy chạy vuông góc với hướng của khuyết tật cần được phát hiện.
V.2. Sự lan truyền của dòng xoáy
2.1. Trường hợp chi tiết phẳng
Đưa cuộn dây có dòng điện xoay chiều chạy qua lại gần chi tiết kim loại. Dòng điện i được tính bằng công thức:
i = Io.sin (t)
Dòng xoáy được tạo ra trong chi tiết và lan truyền xuống dưới bề mặt.
Những dòng xoáy đó gồm các dòng điện ic chạy ở các độ sâu khác nhau trong chi tiết.
Sự tính toán bằng lý thuyết không dẫn thẳng đến cường độ dòng điện ic mà mật độ của dòng Jc.
Mật độ của dòng Jc thể hiện mật độ dòng qua một phần nhỏ bề mặt s nằm vuông góc với các dòng điện.
Mối liên hệ giữa Jc và ic được thể hiện qua công thức
Jc = ic/s
Giả thiết rằng từ trường cảm ứng He được tạo bởi cuộn dây là đều (không đúng), có thể chỉ ra rằng mật độ và pha của dòng xoáy thay đổi phụ thuộc vào độ sâu p trong chi tiết.
Tại độ sâu p trong chi tiết, mật độ Jc được tính như sau:
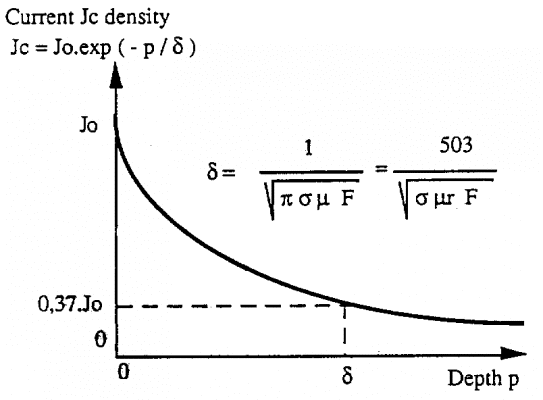
Jc = Jo.exp (-p/).sin (t-)
Trong đó Jo là mật độ dòng xoáy trên bề mặt (p = 0)
Công thức trên có thể chia làm 2 phần:
Phần 1: exp(-p/) thể hiện sự suy giảm mật độ theo chiều sâu
Phần 2: sin (t-) thể hiện sự thay đổi pha của dòng xoáy theo chiều sâu.
Nhớ rằng là pha của dòng xoáy. Dòng xoáy có cùng , tức là cùng tần số với dòng chạy trong cuộn cảm.
2.1.1. Độ sâu truyền quy ước
Sự suy giảm của mật độ dòng xoáy được đặc trưng bởi hàm mũ, thể hiện qua đồ thị sau:
có tên gọi là độ sâu truyền quy ước, là chiều sâu mà ở đó mật độ Jc bằng mật độ Jo ở bề mặt chia cho e = 2,718
Jc = Jo / e = 0.37.Jo
Mật độ ở độ sâu đó chỉ bằng 37% mật độ ở bề mặt
Độ sâu truyền quy ước phụ thuộc vào điều kiện kiểm tra và bản chất của chi tiết.
Nó được tính bằng công thức:
= 1/ ...F
Trong đó là độ dẫn điện của chi tiết
là độ từ thẩm của chi tiết
F là tần số kiểm tra
thay bằng độ từ thẩm tương đối r, ta có:
= 503/ .r.F
Sau đây là một số ví dụ tính độ sâu truyền quy ước:
– Đối với vật liệu phi từ tính r = 1, độ dẫn điện của hợp kim nhôm = 25,4 MS/m
• Với tần số F = 1 kHz = 1000 Hz
= 503/ 25,4.106 .103 = 0.0031 m = 3.1 mm
• Với tần số F = 1 MHz = 1.000.000 Hz
= 503/ 25,4.106 .106 = 0.0001 m = 0.1 mm
– Ta xem xét hai chi tiết gần giống nhau về độ dẫn điện nhưng một chi tiết là phi từ tính còn chi tiết kia là từ tính.
* thiếc r = 1, = 7,7 MS/m
với F = 1 kHz = 1000 Hz
= 503/ 7,7.106 .103 = 0.0057 m = 5.7 mm
* thép r = 1000, = 8 MS/m
với tần số F = 1 kHz = 1000 Hz
= 503/ 8.106 .103 .103= 0.0002 m = 0.2 mm
Chúng ta ghi nhớ rằng:
Độ dẫn điện, độ từ thẩm, tần số càng tăng thì độ sâu truyền quy ước giảm. Đó là hiệu ứng bề mặt.
Nếu chúng ta muốn phát hiện khuyết tật gần hoặc khuyết tật mở trên bề mặt, chúng ta sẽ sử dụng dòng có tần số cao.
Nếu chúng ta muốn phát hiện khuyết tật nằm dưới sâu, cần thiết đạt được độ sâu truyền lớn hơn, chúng ta sẽ sử dụng dòng có tần số thấp hơn.
Đối với chi tiết bằng vật liệu sắt từ với độ từ thẩm cao hơn nên độ truyền sâu của dòng xoáy rất thấp. Chi tiết bằng vật liệu sắt từ khó kiểm tra hơn so với vật liệu phi từ tính.
Chúng ta đã biết từ chương 2 rằng, khi vật liệu sắt từ đạt tới mức bão hòa từ, độ từ thẩm r của chúng giảm dần tới gần giá trị 1
Kỹ thuật bão hòa từ cho vật liệu sắt từ có thể sử dụng để tăng độ sâu truyền của dòng xoáy để phát hiện các khuyết tật nằm dưới sâu.
Ghi chú:
Độ sâu truyền quy ước theo lý thuyết chỉ áp dụng với vật dẫn phẳng, kích thước không hạn chế, đưa vào từ trường đều He (có cùng hướng và cùng giá trị ở mọi điểm trên vật dẫn).
Trong thực tế, công thức đó có thể ứng dụng với các chi tiết không phẳng, và ta cũng tạo từ trường không đều. Nên công thức đó ứng dụng với ít nhiều tính hiệu lực.
Cuối cùng, để xác định Độ sâu truyền quy ước , có thể sử dụng biểu đồ, trong đó Độ sâu truyền quy ước tính bằng mm thay đổi theo tần số F và với các vật liệu khác nhau.
Chúng ta có thể kiểm tra lại từ biểu đồ trên những giá trị mà ta tính toán ở những ví dụ trên.
2.1.2. Thay đổi pha của dòng xoáy:
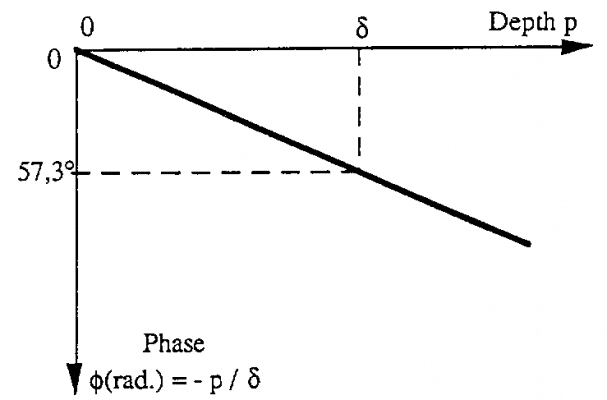
Có thể chỉ ra rằng pha của dòng xoáy tạo trong chi tiết phẳng bởi từ trường đều, thay đổi tuyến tính với độ sâu p:
được tính bằng công thức:
(radian) = -p/
Đồ thị sau biểu diễn sự thay đổi theo p
Khi p = thì = -1 radian = -57,30
Ghi chú:
Nếu thay bằng công thức tính của nó, ta có thể viết;
= -p. ...F
Nếu tần số lớn hơn thì pha giữa dòng xoáy chạy trong chi tiết và trên bề mặt sẽ lớn hơn.
Trong thực tế, hiện tượng này có thể sử dụng để phân biệt những hiệu ứng liên quan đến khuyết tật nằm trong và trên bề mặt.
Chúng ta phải có sự cân đối giữa sự lệch pha và độ sâu truyền.
Chúng ta sẽ chọn tần số cao để thu được sự lệch pha lớn nhưng cũng phải đủ độ sâu truyền nếu chúng ta muốn phát hiện những khuyết tật nằm trong chi tiết.
Xác định tần số tối ưu đạt được bằng thực nghiệm.
2.2. Trường hợp thanh trụ
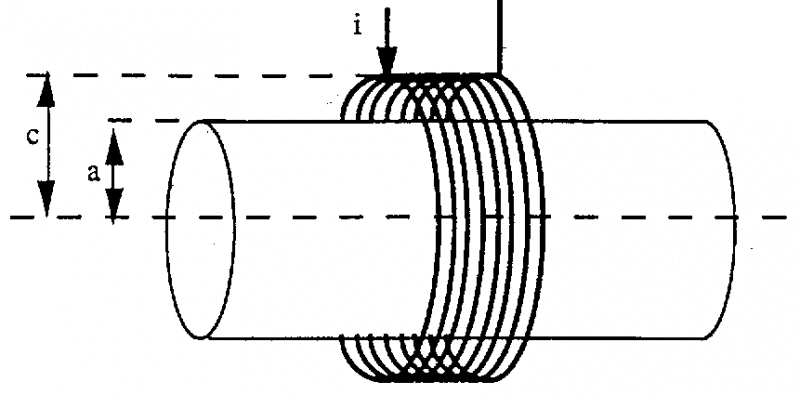
Chúng ta có thanh trụ, chiều dài không hạn chế, độ dẫn điện và độ từ thẩm là hằng số, đặt trong ống dây, cả hai đồng trục:
a bán kính thanh trụ
c bán kính ống dây
n số vòng dây trên một đơn vị chiều dài ống dây
i cường độ dòng điện chạy trong ống dây: i = Io.sin (t)
Từ trường tạo bởi ống dây là:
H = n.i
Mật độ dòng xoáy Jc tạo ra tại điểm P trong thanh trụ được tính bằng công thức phức tạp sau:
Jc = k.n.Io.M1 (kr)/Mo(ka).sin (t – )
trong đó: k = 1/ 2....F
r là khoảng cách từ điểm P tới trục của thanh trụ (0 r a)
Mo và M1 là hàm số Bessel
Ta thấy rằng mật độ và pha của dòng xoáy thay đổi theo vị trí của điểm P.
Sự thay đổi mật độ được tính bằng:
k.n.Io.M1 (kr)/Mo(ka)
Sự thay đổi pha được tính bằng:
= 1 (kr) – o(ka)
trong đó 1 và o là hàm số Bessel.
2.2.1. Số đối chứng ka
Thanh trụ được đặc trưng bởi Số đối chứng ka
Số này không có đơn vị.
ka= a/ 2....F
Ta thấy rằng ka phụ thuộc vào:
– Kích thước hình học của thanh trụ (bán kính a)
– Bản chất vật liệu (độ dẫn điện, độ từ thẩm…)
– Tần số kiểm tra
2.2.2. Tần số đặc trưng Fg
Từ số đối chứng ka, ta có thể định nghĩa Tần số đặc trưng Fg như sau:
ka = F/Fg
Khi F = Fg, ka = 1
Fg = a2/2....
hay Fg = d2/...8
Ghi chú:
Nếu thay bằng r ta có:
Fg = 506600/
2.2.3. Sự thay đổi mật độ của dòng xoáy
Ta biết rằng Sự thay đổi mật độ được tính như sau:
k.n.Io.M1 (kr)/Mo(ka)
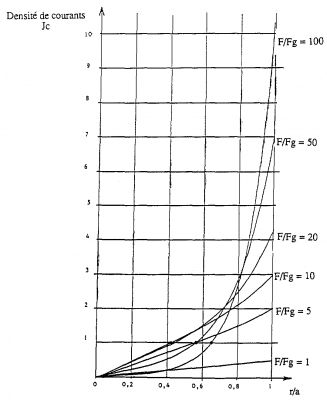
Sơ đồ sau cho thấy Sự thay đổi mật độ của dòng xoáy phụ thuộc khoảng cách r/a cho các tần số khác nhau, khác nhau về tỷ số F/Fg.
Đồ thị trên được vẽ trong trường hợp giá trị từ trường H = n.Io 1 A/m
Kết quả thu được tương đương với chi tiết phẳng.
Tỷ số F/Fg càng lớn thì mật độ dòng xoáy trên bề mặt càng lớn. Điều đó có nghĩa là độ nhạy với khuyết tật bề mặt càng lớn.
2.2.4. Sự thay đổi pha
Sự thay đổi pha được tính bằng:
= 1 (kr) – o(ka)
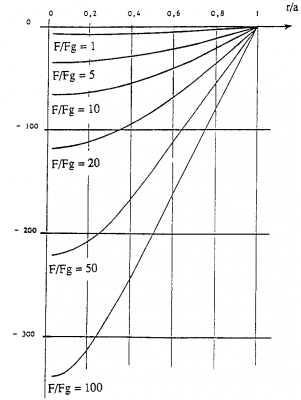
Sơ đồ sau cho thấy Sự thay đổi pha của dòng xoáy phụ thuộc khoảng cách r/a cho các tần số khác nhau, khác nhau về tỷ số F/Fg.
Tỷ số F/Fg càng lớn thì chênh lệch pha giữa dòng xoáy trên bề mặt và dòng xoáy chạy ở trong chi tiết càng lớn.
Ghi chú: cũng như đối với vật dẫn phẳng, hiện tượng này có thể sử dụng để phân biệt rõ những hiệu ứng liên quan đến khuyết tật nằm trong và trên bề mặt.
2.2.5. Độ sâu truyền
Chúng ta gọi độ sâu truyền quy ước, là chiều sâu mà ở đó mật độ Jc bằng mật độ Jo ở bề mặt chia cho e = 2,718
Trong trường hợp chi tiết phẳng độ sâu truyền quy ước được tính bằng công thức:
= 1/ ...F
Không có công thức đơn giản cho thanh trụ.
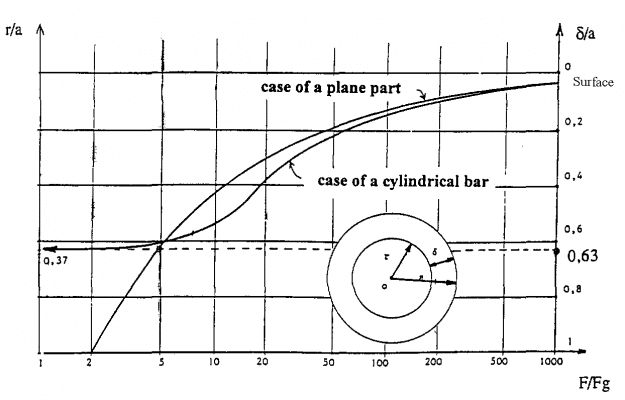
Đồ thị dưới đây biểu diễn sự thay đổi theo tỷ số F/Fg.
Ta thấy tỷ số F/Fg càng nhỏ thì độ sâu truyền quy ước càng lớn.
Ta cũng nhận thấy rằng độ sâu truyền quy ước không thể lớn hơn 0,63a trong bất kỳ trường hợp nào.
Điều đó có nghĩa là vùng tâm của thanh trụ (r < 0,37a) không thể kiểm tra bằng phương pháp dòng xoáy kể cả trường hợp sử dụng tần số thấp nữa.
Trên đồ thị có vẽ cả đường cong tương ứng độ sâu truyền quy ước trên chi tiết phẳng.
Ta nhận thấy rằng công thức cho chi tiết phẳng có thể sử dụng, dưới điều kiện nhất định, để xác định giá trị xấp xỉ của độ sâu truyền quy ước trong thanh trụ.
Thực tế ta thấy rằng:
– Nếu F/Fg > 100 giá trị thu được với chi tiết phẳng và thanh trụ gần như nhau, chỉ khác số ít phần trăm
– Nếu 5 < F/Fg < 100 sai số nhỏ hơn 20%
– Nếu F/Fg < 5 giá trị thu được với chi tiết phẳng không thể sử dụng cho thanh trụ
2.2.6. Ý nghĩa của tần số đặc trưng Fg
Tần số đặc trưng Fg cho thanh trụ tương ứng với tần số mà dưới nó độ sâu truyền quy ước của dòng xoáy đạt giá trị cao nhất.
Nó còn được gọi là tần số giới hạn.
2.3. Trường hợp ống tuýp
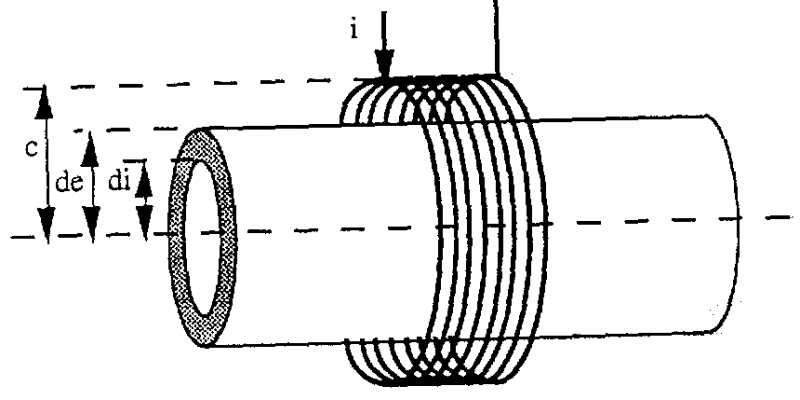
Ta có vật dẫn dạng ống, chiều dài không hạn chế, độ dẫn điện và độ từ thẩm là hằng số, đặt trong ống dây, cả hai đồng trục:
Trong đó di là đường kính trong của ống
de là đường kính ngoài của ống
2.3.1. Tần số đặc trưng Fc:
Như trường hợp thanh trụ, có thể định nghĩ tần số đặc trưng của ống tuýp dày.
Nó được tính bằng công thức:
Fc = 2/...de2 = 506600/.r.de2
trong đó tính bằng S/m
de tính bằng m
Fc tính bằng Hz
hoặc: Fc = 506,6.106/.r.de2
trong đó tính bằng S/m
de tính bằng mm
Fc tính bằng kHz
Ghi chú: Trong trường hợp ống dày kiểm tra bằng cuộn dây trong,tần số đặc trưng được tính bằng công thức:
Fc = 2/...di2 = 506600/.r.di2
trong đó tính bằng S/m
di tính bằng m
Fc tính bằng Hz
hoặc: Fc = 506,6.106/.r.di2
trong đó tính bằng S/m
di tính bằng mm
Fc tính bằng kHz
2.3.2. Mật độ và pha của dòng xoáy:
– Ji và Je là mật độ mặt trong và ngoài của ống
– i và e là pha của dòng xoáy ở độ mặt trong và ngoài của ống
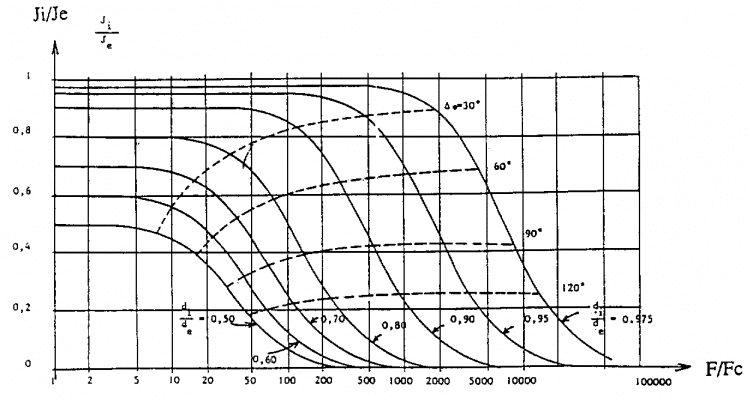
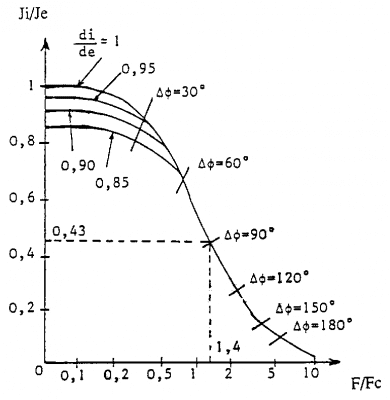
Sau đây là sơ đồ biểu diễn sự thay đổi của tỷ số Ji/Je cũng như sự lệch pha
e – i theo sự thay đổi của tỷ số F/Fc và di/de
Theo sơ đồ, với ống xác định, F/Fc càng lớn Ji/Je càng nhanh tiến tới 0.
Có nghĩa là khi ta sử dụng ống dây, F/Fc lớn, mật độ dòng xoáy trên mặt ngoài ống sẽ lớn, độ sâu truyền của dòng xoáy thấp.
Ta cũng thấy rằng tỷ số F/Fc càng lớn thì chênh lệch pha càng lớn.
Ta thấy rằng giống như trong trường hợp thanh trụ.
Sự lựa chon tần số cũng sẽ là cân đối giữa sự lệch pha và độ sâu truyền để phân biệt đúng đắn những hiệu ứng từ khuyết tật trong và ngoài.
2.3.3. Trường hợp ống tuýp mỏng:
Trong trường hợp ống tuýp mỏng, có thể sử dụng công thức khác để xác định tần số đặc trưng. Đó là công thức GUERIN:
Fc = 2/...di.e
Trong đó e = chiều dày ống
Ta có thể viết:
Fc = 506600/.r.di .e
Trong đó tính bằng S/m
di, e tính bằng m
Fc tính bằng Hz
hoặc: Fc = 506,6.106/.r.di.e
Trong đó tính bằng S/m
di, e tính bằng mm
Fc tính bằng kHz
Bên cạnh đó B.DAVID và M.PIGEON đưa ra công thức khác để tính tần số đặc trưng cho ống mỏng (di/de > 0,85):
Fc = 2,5.105/.r.e
trong đó tính bằng S/m
e tính bằng mm
Bằng cách này, tần số đặc trưng không phụ thuộc vào đường kính trong và ngoài của ống tuýp. Nó chỉ phụ thuộc vào chiều dày của ống và bản chất của vật liệu.
Sơ đồ sau biểu diễn sự liên quan giữa mật độ Ji,và Je và độ lệch pha e – i theo tỷ số F/Fc
Ta thấy rằng khi F/Fc = 1.4, độ lệch pha giữa dòng chạy mặt trong và ngoài là 900, tỷ lệ mật độ = 0.43 và nó không phụ thuộc vào kích thước hình học của ống (dưới điều kiện di/de > 0,85 )
V.3. Định luật về tính tương tự
Thực tế khi những sản phẩm có kích thước hình học tương tự được đặt trong điều kiện kiểm tra tương đương, ta thấy sự phân bố dòng xoáy tương tự.
Dựa trên sự tương tự đó, sự diễn giải hiệu ứng liên quan tới sự thay đổi của một vài yếu tố có thể chuyển từ sản phẩm này sang sản phẩm khác.