1. Khái Niệm về lượng giác

Hàm lượng giác là các hàm toán học của góc, được dùng khi nghiên cứu tam giác và các hiện tượng có tính chất tuần hoàn. Các hàm lượng giác của một góc thường được định nghĩa bởi tỷ lệ chiều dài hai cạnh của tam giác vuông chứa góc đó, hoặc tỷ lệ chiều dài giữa các đoạn thẳng nối các điểm đặc biệt trên vòng tròn đơn vị. Chúng cũng được biểu diễn bằng các chuỗi (toán học) hoặc là nghiệm của một số phương trình vi phân, và có thể được mở rộng để nhận giá trị âm (toán học) hoặc số phức.

2. Tam Giác Vuông và các hàm lượng giác

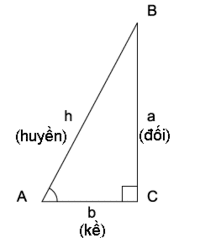
Một tam giác vuông luôn chứa một góc 90° (π/2 radian), được ký hiệu là C trong hình này. Góc A và B có thể thay đổi. Các hàm lượng giác thể hiện mối liên hệ chiều dài các cạnh và độ lớn các góc của tam giác vuông.

Có thể định nghĩa các hàm lượng giác của góc A, bằng việc dựng nên một tam giác vuông chứa góc A. Trong tam giác vuông này, các cạnh được đặt tên như sau:
  • Cạnh huyền là cạnh đối diện với góc vuông, là cạnh dài nhất của tam giác vuông, h trên hình vẽ.
  • Cạnh đối là cạnh đối diện với góc ㅏ, a trên hình vẽ.
  • Cạnh kề là cạnh nối giữa góc ㅏ và góc vuông, b trên hình vẽ.

Dùng hình học Ơclit, tổng các góc trong tam giác là pi radian (hay 180⁰). Khi đó:

Hàm Định nghĩa Biểu thức
Sin Cạnh đối chia cho cạnh huyền \sin A={\frac {a}{h}}
Cos Cạnh kề chia cho cạnh huyền \cos A={\frac {b}{h}}
Tang Cạnh đối chia cho cạnh kề \tan A={\frac {a}{b}}
Cotang Cạnh kề chia cho cạnh đối \cot A={\frac {b}{a}}
Sec Cạnh huyền chia cho cạnh kề \sec A={\frac {h}{b}}
Cosec Cạnh huyền chia cho cạnh đối \csc A={\frac {h}{a}}

 

 

 

 

 

 

 

 

 

 

 

Tổng kết lại công thức, chúng ta có mẹo để nhớ như sau: Sin đi học, cốt không hư, tan đoàn kết cotan kết đoàn

3. Định lý Pitago

(Cạnh huyền)2 = (cạnh góc vuông thứ nhất)2 + (Cạnh góc vuông thứ 2)2

h2 = a2 + b2