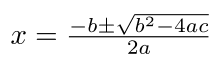I. ĐẠI SỐ LÀ GÌ

Đại số bắt đầu với các tính toán tương tự như số học, với chữ cái thay cho chữ số. Điều này cho phép chứng minh các định lý hay công thức là đúng mà không phải quan tâm đến các số có liên quan. Ví dụ, trong phương trình bậc hai

ax²+bx+c=0
a, b, c có thể là bất kỳ số nào (ngoại trừ a phải khác 0), và công thức giải phương trình bậc hai có thể được sử dụng nhanh chóng và dễ dàng tìm thấy những giá trị của biến số x.

Trong quá trình phát triển, đại số đã được mở rộng đến các đối tượng không phải số khác, chẳng hạn như vectơ, ma trận và đa thức. Sau đó, các thuộc tính cấu trúc của các đối tượng không phải số này được tóm tắt để xác định các cấu trúc đại số như nhóm, vành và trường.

Trước thế kỷ 16, toán học được chia thành hai lĩnh vực số học và hình học. Mặc dù một số phương pháp đã được phát triển từ trước, có thể được coi là đại số, nhưng sự xuất hiện của đại số, và không lâu sau đó, các phép vi phân và tích phân như một lĩnh vực của toán học chỉ có từ thế kỷ 16 hoặc 17. Từ nửa sau của thế kỷ 19 trở đi, nhiều lĩnh vực mới của toán học xuất hiện, hầu hết trong số đó đã sử dụng cả số học và hình học, và gần như tất cả trong số đó đều sử dụng đại số.

II. CÁC HẰNG ĐẲNG THỨC ĐẠI SỐ CƠ BẢN

1. Bình phương của một tổng:

(a + b)² = a² + 2ab + b²  → a² + b² = (a + b)² − 2ab

2. Bình phương của một hiệu:

(a − b)² = a² − 2ab + b² → a² – b² = (a + b)² + 2ab

3. Hiệu hai bình phương:

a²  − b² = (a + b)(a − b)

4. Lập phương của một tổng:

(a + b)³ = a³ + 3a²b + 3ab² + b³ → a³ + b³ = (a + b)³ − 3ab(a + b)

5. Lập phương của một hiệu:

(a − b)³ = a³ − 3a²b + 3ab² − b³

6. Tổng hai lập phương:

a³ + b³ = (a + b)(a² − ab + b²)

7. Hiệu hai lập phương:

a³ − b³ = (a − b)(a² + ab + b²)

III. CÁC PHƯƠNG TRÌNH ĐẠI SỐ

1. Phương trình tuyến tính

Phương trình tuyến tính (hay còn gọi là phương trình bậc một hay phương trình bậc nhất) là một phương trình đại số có dạng:

f(x)=ax+b=0

b là một hằng số (hay hệ số bậc 0).
a là hệ số bậc một.

Phương trình bậc một được gọi là phương trình tuyến tính vì đồ thị của phương trình này là đường thẳng (theo Hán-Việt, tuyến nghĩa là thẳng).

2. Phương trình bậc hai

Trong đại số sơ cấp, phương trình bậc hai là bất kỳ phương trình có dạng:

ax²+bx+c=0
với x là ẩn số chưa biết và a, b, c là các số đã biết sao cho a khác 0. Nếu a = 0 thì phương trình sẽ chuyển về dạng bậc nhất, không còn là bậc hai. Các số a, b, và c là những hệ số của phương trình và có thể phân biệt bằng cách gọi tương ứng hệ số bậc hai, hệ số bậc một, và hằng số hay số hạng tự do.

Vì phương trình bậc hai chỉ có một ẩn nên nó được gọi là phương trình “đơn biến”. Phương trình bậc hai chỉ chứa lũy thừa của x là các số tự nhiên, bởi vậy chúng là một dạng phương trình đa thức, cụ thể là phương trình đa thức bậc hai do bậc cao nhất là hai.
Công thức nghiệm tổng quát của phương trình bậc hai