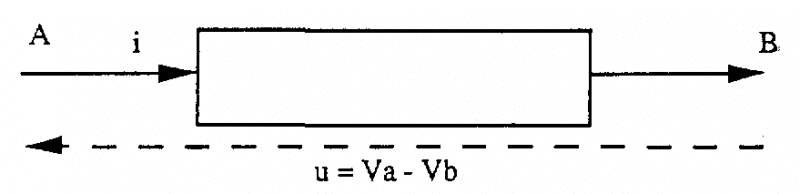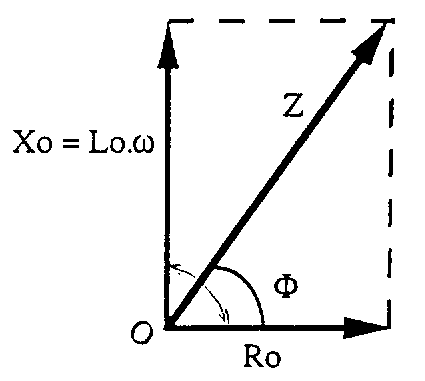第III章:電気の基礎理論
III.1. Nguyên lý chung
1.1. Dòng điện
Chúng ta gọi dòng điện hay điện là hiện tượng liên quan đến sự dịch chuyển của điện tích (điện tử hay ion) trong vật dẫn.
Trong phần lớn các trường hợp thường xảy ra đặc biệt là trong trường hợp dòng điện sử dụng trong kiểm tra bằng phương pháp dòng xoáy, nó liên quan đến sự dịch chuyển của các điện tử trong các kim loại rắn, chúng có thể là dây đồng tạo đầu dò hoặc chi tiết ( làm từ nhôm, thép…).
Cũng có một số vật liệu composite có thể dẫn điện, ví dụ như sợi các bon, ở đó sự dịch chuyển của các điện tử được thực hiện bởi sợi các bon dẫn điện.
1.2. Cường độ dòng điện
Cường độ dòng điện (i) là đại lượng liên quan tới sự dịch chuyển của các điện tử trong vật dẫn.
Đơn vị Cường độ dòng điện là Ampe (A)
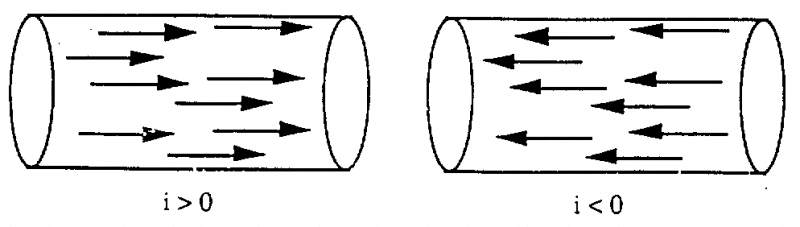
Cường độ dòng điện có thể dương hoặc âm khi dấu – xuất hiện, điện tử dịch chuyển theo chiều ngược khi có dấu +
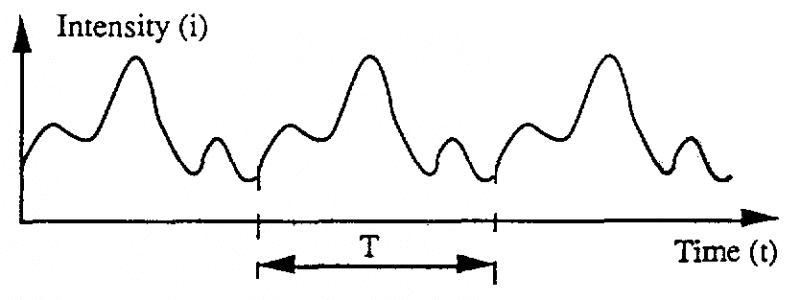
1.3. Dòng thay đổi – dòng tuần hoàn
Chúng ta gọi dòng thay đổi là dòng có cường độ thay đổi theo thời gian
Chúng ta gọi dòng tuần hoàn là dòng thay đổi với sự thay đổi cường độ tái xuất hiện đúng thời gian.
Thời gian giữa hai sự kiện gần nhau mà cường độ dòng điện có cùng giá trị được gọi là chu kỳ (T).
Đơn vị của chu kỳ là giây (s)
Chúng ta cũng định nghĩa tần số F. Tần số F tương ứng với số chu kỳ trong 1 giây.
Đơn vị của tần số là Hertz (Hz)
F và T liên quan bởi công thức:
F = 1/T
Ví dụ dòng thay đổi hình sin là dòng chu kỳ.
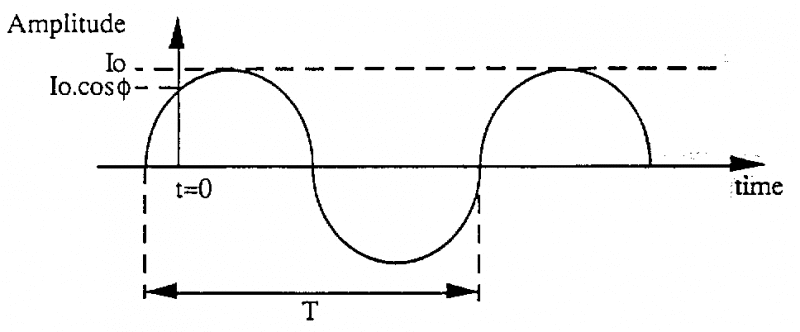
1.4. Dòng hình sin
Những dòng này có cường độ biểu diễn là hàm theo thời gian
i = Io .cos (.t + )
Io cường độ dòng điện cực đại
= 2./T = 2..F
được biểu diễn bằng radian/giây (rd/s)
pha thời gian bắt đầu (t=0)
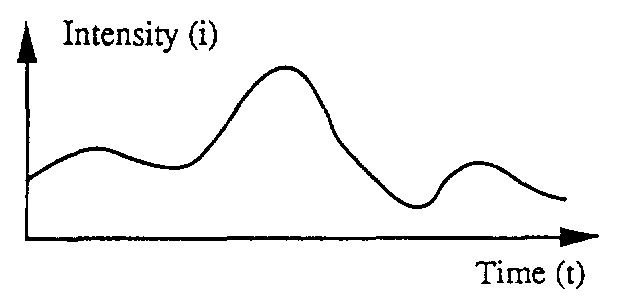
Sơ đồ sau biểu thị cường độ dòng hình sin
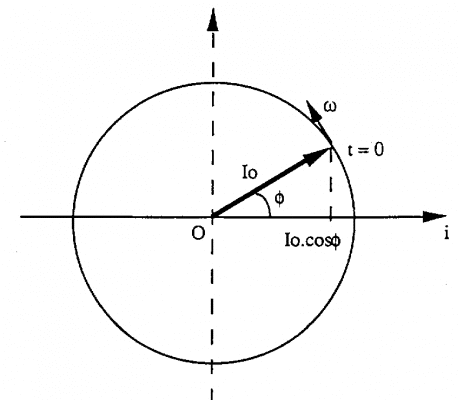
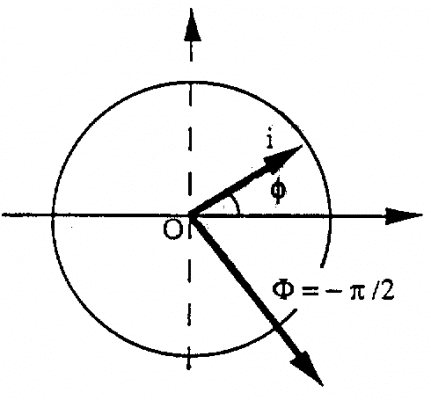
1.5. Sơ đồ Fresnel
Dòng hình sin có thể được biểu diễn bởi vectơ có độ dài Io, quay quanh điểm tâm o. Tại vận tốc góc và tạo góc với trục hoành bằng góc pha tại thời điểm T=0
Cường độ của dòng được tính bằng hình chiếu của vectơ trên trục hoành.
1.6. Sự lệch pha giữa các dòng hình sin
Hai dòng hình sin cho trước bởi công thức:
i1 = Io .cos (.t + 1)
i2= Io .cos (.t + 2)
Những dòng này có cùng biên độ và lệch pha tại thời điểm t=0, nhưng có cùng , tức là cùng tần số
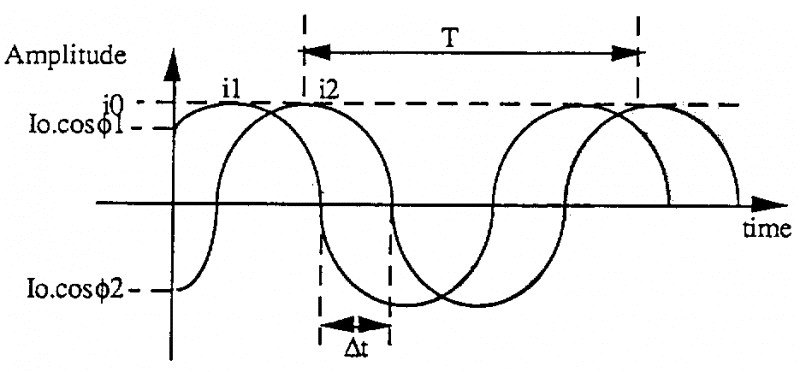
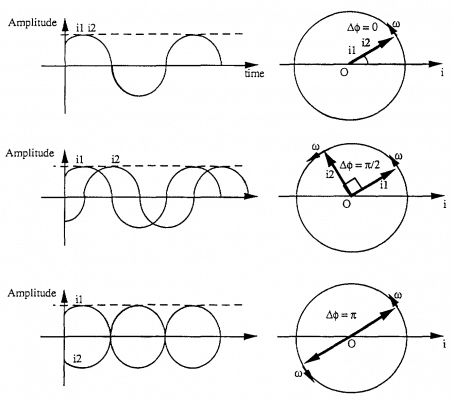
Cường độ theo thời gian của các dòng đó được biểu diễn bằng sơ đồ sau:
Chúng ta thấy rằng các dòng này lệch theo thời gian. Ta nói dòng i1 sau dòng i2
Sự xuất hiện thời gian chậm t giữa hai dòng được gọi là lệch pha
Nếu chúng ta sử dụng sơ đồ Fresnel tại thời điểm t=0, cả hai dòng được biểu diễn bằng 2 vectơ i1 và i2 có cùng độ dài và quay cùng tốc độ. Nó xuất hiện góc hở giữa 2 vectơ i1 và i2:
= 2 – 1
và t liên quan bởi công thức:
= 2.t/T
Ghi chú:
Khi = 0, có nghĩa là các dòng cùng pha
Khi = /2, có nghĩa là các dòng vuông góc
Khi = , có nghĩa là các dòng có pha ngược nhau
Sơ đồ sau biểu diễn các trường hợp đó:
III.2. Kiến thức cơ bản về điện trở – Định luật Ôm
Điện trở của dây dẫn hay của một mạch điện đặc trưng khả năng của dây dẫn hay của một mạch điện truyền tải điện.
Có dòng điện i = Io .cos (.t + ) chạy qua dây dẫn giữa hai điểm A và B.
Dưới tác động của dòng điện, xuất hiện một hiệu điện thế u = Va – Vb
Điện áp u có thể tính một cách tổng quát:
u = Uo .cos (.t + )
Điện áp u cũng hình sin và có cùng tần số với dòng điện i. Tuy nhiên dòng i và điện áp u không phải lúc nào cũng cùng pha
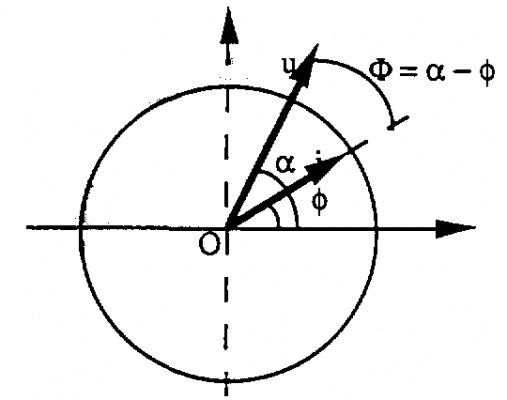
Độ lệch pha giữa u và i là:
= –
Điện áp u cũng có thể biểu diễn trên sơ đồ Fresnel
Ta có sơ đồ sau:
Công thức cho phép chúng ta tính điện thế u từ dòng điện i được gọi là định luật Ôm:
U = Z.i
Trong đó Z được gọi là trở kháng
Đơn vị trở kháng là Ohm ()
Trở kháng của dây dẫn hay của một mạch điện phụ thuộc vào bản chất của vật liệu, nhiệt độ và dạng mạch điện.
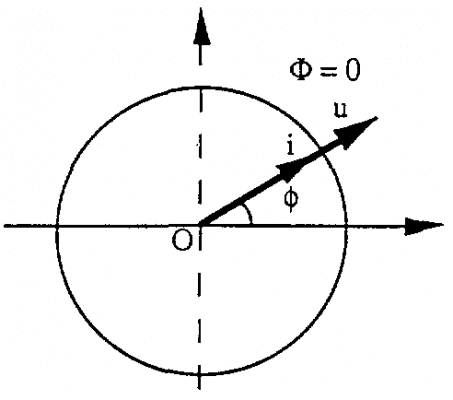
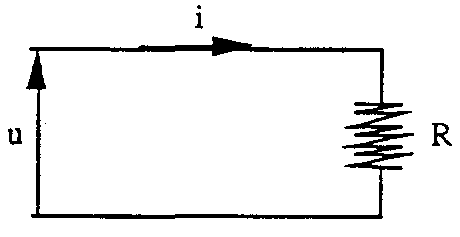
2.1. Điện trở thuần
Khi dòng điện chạy qua dây dẫn (trường hợp dây dẫn thẳng), ta nhận thấy rằng điện thế xuất hiện ở các đầu mút có cùng pha với dòng điện.
Trong trường hợp này, chúng ta nói trở kháng của dây dẫn là điện trở thuần, gọi là điện trở R:
Z = R
Trong mạch điện, điện trở được vẽ như sau:
Điện trở của dây dẫn có thể tính dựa trên tính chất điện của vật liệu và kích thước của dây dẫn:
R = .l/S
Trong đó: là điện trở xuất của vật liệu
l là chiều dài của dây dẫn
S là tiết diện của dây dẫn
Đơn vị của điện trở là Ohm ()
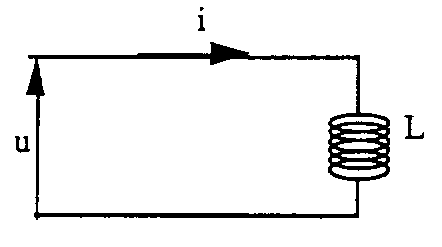
2.2. Độ tự cảm
Ta làm một cuộn dây từ dây dẫn có điện trở bằng 0 (hoặc rất nhỏ)
Cuộn dây như vây được đặc trưng bởi độ tự cảm L:
L = o.N2.S/l
Trong đó: o là độ từ thẩm trong chân không
N là số vòng dây trong cuộn dây
S là tiết diện của sợi dây
l là chiều dài của cuộn dây
Đơn vị của độ tự cảm là Henry (H)
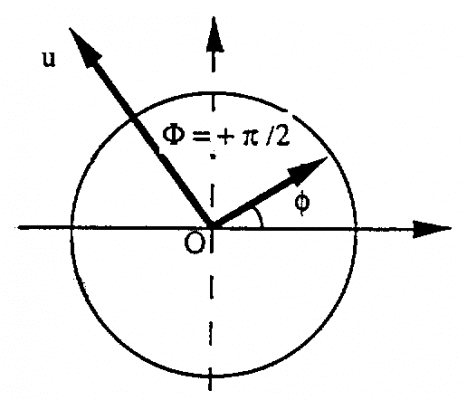
Khi dòng điện chạy qua cuộn dây, ta nhận thấy rằng điện thế xuất hiện ở các đầu mút dẫn trước dòng điện i với độ lệch pha 90 0
Trong trường hợp này, chúng ta gọi đó là cảm kháng XL. Được biểu diễn bằng công thức:
Z = XL = L. = 2..F.L
Đơn vị của cảm kháng là Ohm ()
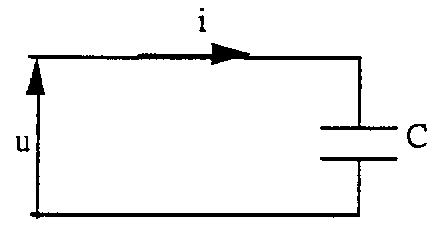
2.3. Điện dung
Chúng ta gọi tụ điện là thiết bị gồm 2 tấm kim loại riêng rẽ bởi chất cách điện giữa chúng.
Khi dòng điện chạy qua tụ điện, nó có đặc tính tích điện. Tụ điện được xác định bởi điện dung C
Đơn vị của điện dung là Farad (F)
Dưới tác động của dòng điện chay qua, điện thế xuất hiện ở tự điện châm pha so với dòng điện i là 90 0.
Trong trường hợp này, chúng ta gọi đó là dung kháng Xc. Được biểu diễn bằng công thức:
Z = Xc= -1/(C.)
Đơn vị của dung kháng là Ohm ()
2.4. Cuộn dây trong thực tế
Trong thực tế, điện trở của cuộn dây không bao giờ bằng không
Chính vì vậy chúng ta phải tính đến điện trở thuần của dây dẫn của cuộn dây và độ tự cảm của nó.
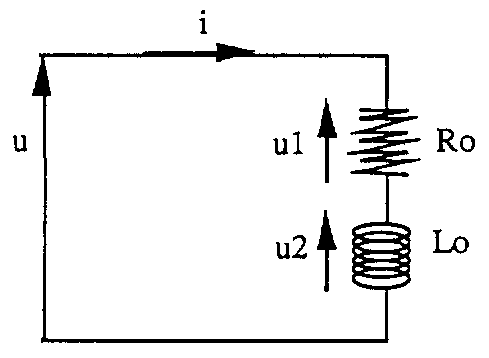
Sơ độ sau biểu diễn các thành phần của cuộn dây.
Ở các điểm cuối của mỗi thành phần xuất hiện từng điện thế
• Ở các điểm cuối của điện trở thuần Ro xuất hiện điện thế u1 = Ro.i
Ở các điểm cuối của tự cảm Lo xuất hiện điện thế u2 = Xo.i = Lo..i
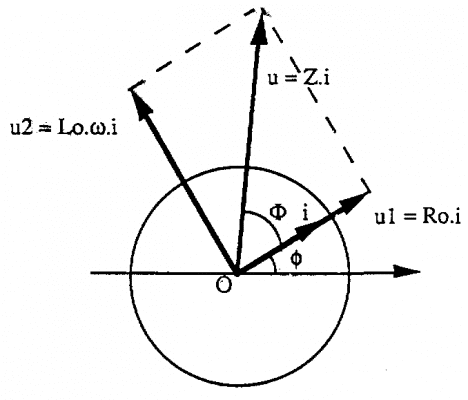
Trên sơ đồ biểu diễn Fresnel, điện áp ở các điểm cuối của cuộn dây bằng tổng vectơ u1 và u2:
u= Zo.i = u1 + u2
Theo định luật Pitago, giá trị của trở kháng có thể tính bằng công thức:
Zo = (Ro2 + Lo2.2)
Bên cạnh đó, độ lệch pha giữa điện thế u và dòng điện i được tính theo công thức:
tg = Lo./Ro
2.5. Sơ đồ trở kháng và ký hiệu số phức
Từ sơ đồ biểu diễn Fresnel, độ dài mỗi cạnh của tam giác vuông tỷ lệ với điện áp u.
Để đơn giản ta chia mỗi cạnh cho i.
Ta thu được sơ đồ trở kháng như sau.
Sơ đồ biểu diễn thành phần trở kháng của cuộn dây thực.
Dạng biểu diễn này có thể chung cho mỗi mạch điện.
Nguyên tắc chung, mỗi mạch có thể chia thành 3 phần đơn giản mà ta đã biết, đó là:
o Điện trở thuần R: Z = R
o Cảm kháng: Z = Xl = L.
o Dung kháng: Z = Xc = -1/C.
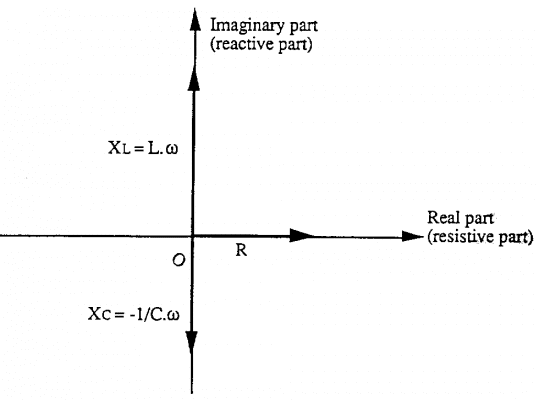
Trên sơ đồ trở kháng
Điện trở thuần được biểu diễn trên trục hoành
Cảm kháng hoặc dung kháng biểu diễn trên trục tung
Cảm kháng biểu diễn theo chiều dương của trục tung
Dung kháng biểu diễn theo chiều âm của trục tung
Nó có thể biểu diễn bằng toán học, gọi là số phức.
Trở kháng trên trục hoành được gọi là phần thực, Trở kháng trên trục tung được gọi là phần ảo.
Theo ký hiệu của số phức
o Điện trở thuần R: Z = R
o Cảm kháng: Z =j.Xl = j.L.
o Dung kháng: Z = Xc = -j/C.
Trở kháng của cuộn dây thực với điện trở thuần Ro và độ tự cảm Lo:
Zo = Ro + j.Xo = Ro + j.Lo.
III.3. Ôn lại một số định luật
3.1. Định luật Joule
Chúng ta gọi hiệu ứng Joule là hiện tượng liên quan tới sự nóng lên của dây dẫn do tác động của dòng điện chạy trong nó.
Hiệu ứng này không phụ thuộc vào chiều dòng điện.
Lượng nhiệt phát ra từ dòng điện:
Tỷ lệ với thời gian dòng điện chạy qua
Tỷ lệ với bình phương cường độ dòng điện
Tỷ lệ với điện trở dây dẫn
Và theo định luật Jul, Lượng nhiệt phát ra từ dòng điện được biểu diễn:
W = R.i2.t
Đơn vị của W là Joule (J)
3.2. Định luật Kirchhoff
3.2.1. Định luật về các điện trở mắc nối tiếp
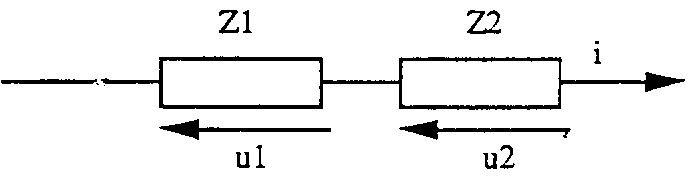
Cho mạch điện có hai điện trở Z1 và Z2 mắc nối tiếp.
Dưới tác động của dòng điện i, các điện áp xuất hiện ở các điểm cuối của các điện trở là u1 và u2.
Điện áp u của mạch được tính bởi công thức:
u = u1 + u2
u = Z1.i + Z2.i
u = (Z1 + Z2).i
Suy ra Z = Z1 + Z2
Khi các điện trở mắc nối tiếp, điên trở tông của cả mạch bằng tổng của các điện trở thành phần.
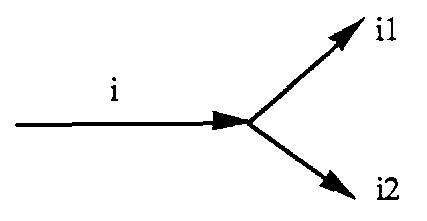
3.2.2. Luật về điểm nút
Chúng ta gọi điểm nút là điểm có các dòng điện vào và ra.
Định luật này phát biểu rằng: tổng các cường độ các dòng điện vào nút bằng tổng các cường độ các dòng điện ra khỏi nút.
I = i1 + i2
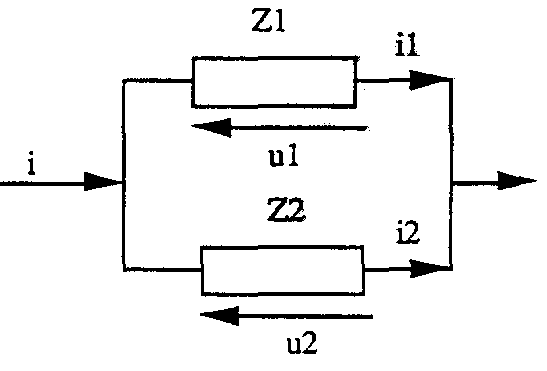
3.2.3. Định luật về các điện trở mắc song song
Ta có mach điện với hai điện trở mắc song song Z1 và Z2
Dòng điện chia thành hai dòng i1 và i2 qua Z1 và Z2
i= i1 +i2
u =u1 hay Z.i = Z1.i1 suy ra i1 = Z.i/Z1
u = u2 hay Z.i = Z2.i2 suy ra i2 = Z.i/Z2
i = Z.i/Z1 + Z.i/Z2
1 = Z/Z1 + Z/Z2
Cuối cùng ta thu được:
Z = Z1.Z2/(Z1 +Z2)
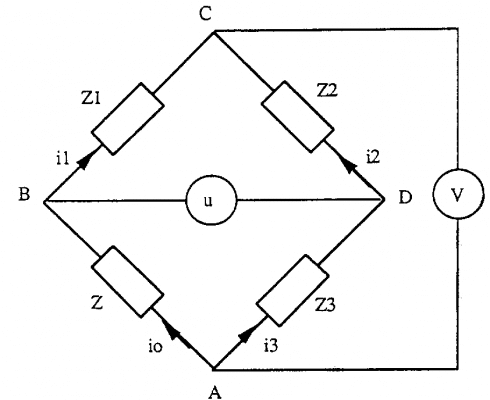
III.4. Cầu Wheatstone
Cầu Wheatstone gồm 4 điện trở mắc theo sơ đồ sau
Chúng ta nói cầu cân bằng khi không có dòng điện chạy qua nhánh BD. Có nghĩa là hiệu điện thế giữa B và D bằng 0, điện thế ở nhánh AB và AD bằng nhau. Từ đó ta có:
Z.io = Z3.i3
Cũng vậy, điện thế ở nhánh BC và DC bằng nhau:
Z1.i1 = Z2.i2
Bên cạnh đó, không có dòng điện chạy qua BD nên i1 = io và i2 = i3
Từ đó ta suy ra
Z.io = Z3.i3
Z1.io = Z2.i3
Vậy Cầu Wheatstone cân bằng khi Z/Z1 = Z3/Z2 hay Z.Z2 = Z1.Z3
Trở kháng của cầu
Ta có thể thấy rằng nếu sự thay đổi một trong các trở kháng của cầu xuất hiện thì điện áp u sẽ khác 0
Điện áp u phụ thuộc vào điện áp V cung cấp cho cầu và sự thay đổi trở kháng Z.
Ta cho rằng trở kháng thay đổi từ Z tới Z + Z
Điện áp u sau đó được tinh như sau:
u = V. Z.Z2.Z3/Z.(Z2 + Z3)2
u = k.V. Z
trong đó k là hệ số cân bằng phụ thuộc vào các điện trở Z2 và Z3